NMR-Spektroskopie

Der Spin

Zur quantenmechanischen Beschreibung von Elektronen dienen seit Schrödinger die so genannten Quantenzahlen. Zur Hauptquantenzahl n, Nebenquantenzahl l und Magnetquantenzahl m gesellt sich eine durch die Lösung der Schrödingergleichung damals nicht näher beschriebene Spinquantenzahl s, die die Werte +1/2 und -1/2 annehmen kann.
Sich den Spin als Eigenrotation des Elektrons vorzustellen hilft nicht wirklich weiter, es genügt, die Tatsache zu akzeptieren, dass atomare Teilchen, die sich in den drei Quantenzahlen n, l und m nicht unterscheiden, dennoch zwei verschiedene Zustände einnehmen können, deren Unterschied sich lediglich im Magnetfeld nachweisen lässt.

Spin von Kernteilchen

Wie bereits angedeutet tragen nicht nur Elektronen einen Spin, auch Kernteilchen haben diese Eigenschaft. Da jeder Kern außer ¹H mehrere Kernteilchen besitzt, entsteht ein Gesamtspin aus den einzelnen Zuständen, der sich genau dann nicht aufheben kann, wenn die Anzahl der Protonen ungerade, die Anzahl der Neutronen ungerade oder beide Werte ungerade sind. Genau solche Atomkerne sind für die chemische Analyse (Kernresonanzspektroskopie) von Bedeutung.

• ¹H – Das Wasserstoffatom mit einem Proton im Kern
• ¹³C – Das Kohlenstoffisotop mit sieben (und nicht sechs) Neutronen im Kern

Diese beiden Kerne können, so wie ein Elektron, gesamt einen Spin von +1/2 oder -1/2 annehmen.

Spininversion

Wird nun ein Magnetfeld von derjenigen Stärke angelegt, die ausreicht, um diesen Spin von +1/2 auf -1/2 umzukehren (Resonanzfrequenz), lässt sich diese Energieaufnahme messen, bzw. in einem Spektrogramm anhand so genannter Peaks ablesen.

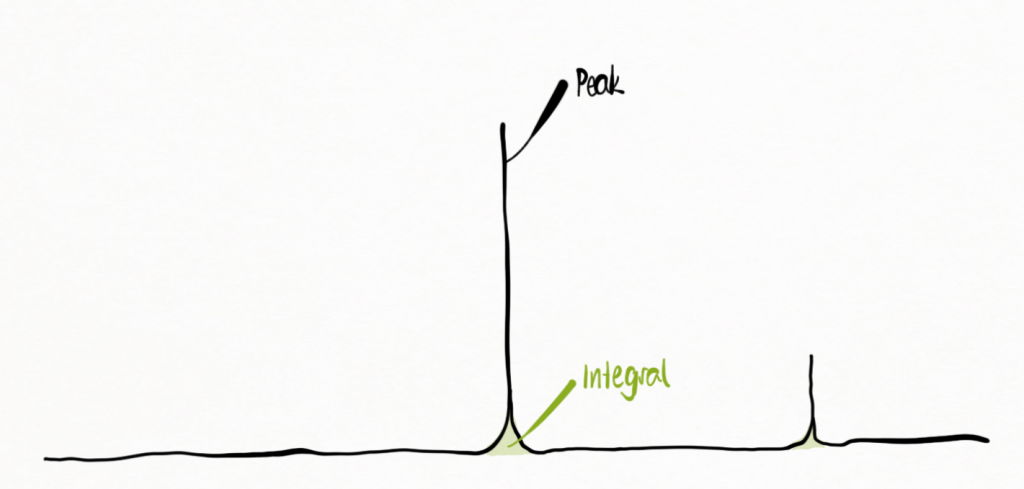Abb. 1   Peaks und deren zugehörige Fläche im NMR Spektrogramm

Molekülanalyse

Sinn zur Molekülanalyse macht die NMR-Spektroskopie aber nur dann, wenn unterschiedlich am Molekül gebundene H-Atome auch mit unterschiedlichen Frequenzen (Frage an KOM: Energien?) angeregt und somit im Spektrogramm unterschieden werden können. Erwartungsgemäß ist genau das der Fall, da es sonst diesen Artikel über diese Form der Analytik nicht geben würde.

Abschirmung – Entschirmung

Je nachdem, wie die Kerne von negativer Ladung umgeben sind, spricht man von mehr oder weniger abgeschirmten Teilchen. Je höher die negative Ladungsdichte ist, desto mehr ist das Proton abgeschirmt. Umgekehrt spricht man von entschirmten Protonen, wenn die Ladungsdichte gering ist. Abgeschirmte Protonen tauchen im Spektrogramm weiter rechts, entschirmte weiter links auf.

Kopplung

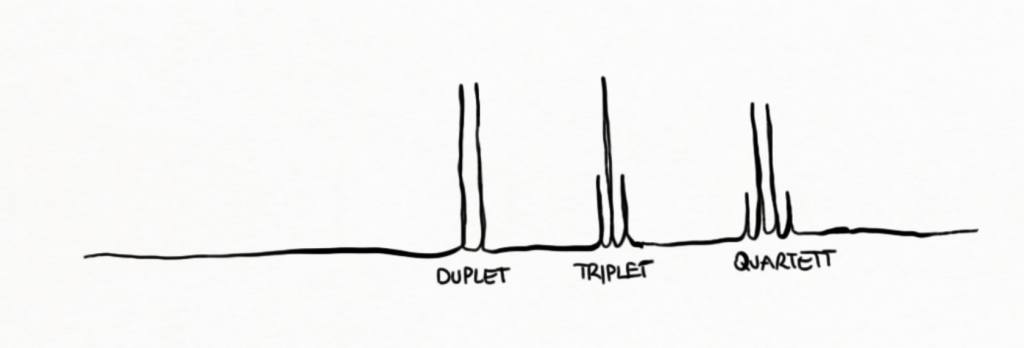
Zusätzlich zur Verschiebung im Spektrum ist auch noch eine zweite Eigenschaft für die Analyse dienlich, nämlich die Kopplung von Protonen mit den Protonen von einem benachbartem C-Atom. Eine Aufspaltung eines Peaks in Duplets, Triplets oder Quartetts erlauben auf einen Rückschluss auf die Anzahl dieser H-Atome in der Nachbarschaft. Peaks werden bei n benachbarten H-Atomen immer in n+1 zusammengehörige Peaks aufgespalten.

 Abb. 2   Aufspaltung in Duplets, Triplets oder Quartetts

Integral

Zuletzt kann man über die Anzahl der betroffenen H-Atome im zu analysierenden Molekül eine Aussage treffen. Allerdings ist hierzu nicht die Peakhöhe, sondern vielmehr die darunter eingeschlossene Fläche die entscheidende Größe. Flächeninhalte werden von den Geräten mit ausgegeben und lassen somit am Ausdruck des Spektrogramms sofort Rückschlüsse zu.

Zusammenfassung

Mit Hilfe der Abschirmung, der Kopplung und dem zugeordneten Integral lassen sich aus Kernresonanzspektrogrammen außerordentliche genau Aussagen über organische Moleküle treffen. Die Struktur von Verbindungen kann mit dieser Methode genau vorausgesagt werden.

Beispiele

Es gibt drei verschieden Arten von H-Atomen in diesem Molekül.